11270. The uncountable ways
There is a rectangle of n ⋅ m units. Another rectangle of a ⋅ b units is cut off from the upper right
corner. Count the number of ways an ant can reach the bottom right corner
starting from the top left corner, if it can move along the grid lines only
right or down.
Input. The first line contains the number of test cases t.
Each of the next t lines contains four integers n, m, a, b (2
≤ n, m ≤ 400000, 1 ≤ a < n, 1 ≤
b < m).
Output. For each test case print on a separate line the number
of ways an ant can reach the bottom right corner under the given conditions.
Print the answer modulo 109 + 7.
|
Sample
input |
Sample
output |
|
3 2 2 1 1 4 5 2 2 7 7 6 6 |
5 105 50 |
SOLUTION
combinatorics
Algorithm analysis
Consider a whole (without cutouts) rectangle of size n * m. Let’s calculate the number of paths from cell (0, 0) to cell (n, m). Since the
path between the specified points has a length of n + m, and at the
same time contains m horizontal segments, the number of paths
is equal to ways(n, m) = 
. If the path is considered as a choice of n vertical
segments from n + m, then the
number of paths is 
. However, note that these values are equal because 
= 
= .
Now consider a
rectangle of size n * m with the right
top cut out of size a * b.
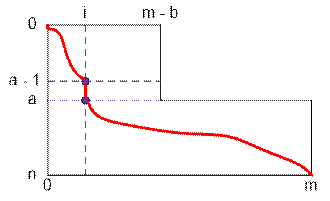
Let’s divide the path from (0,
0) to (n, m) into three
parts:
·
move from (0, 0) to (a – 1, i), where 0 ≤ i ≤ m – b;
·
move from (a – 1, i) to (a, i);
·
move from (a, i) to (n, m);
The number of
paths from (0, 0) to (a – 1, i) is equal to ways(a – 1, i).
The number of
paths from (a,
i) to (n, m) is equal to ways(n – a,
m – i).
Thus the number
of paths from (0, 0) to (n, m) is
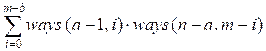
Example
Consider a 2 * 2
rectangle that has a 1 * 1 top right corner cut out. An ant has 5 ways to get
from the top left to the bottom right.
Let’s consider the
second example. From a 4 * 5 rectangle cut out the upper right corner of size 2 * 2.
·
Consider the number of paths from (0, 0) to (1, i), 0 ≤ i ≤
3.
·
Consider the number of paths from (2, i) to (4, 5), 0 ≤ i ≤
3.
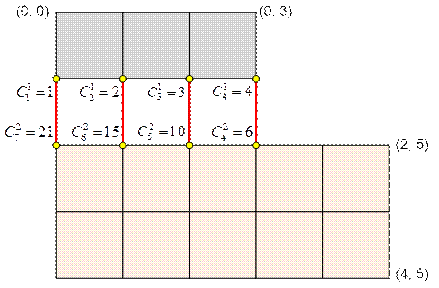
The number of
paths from (0, 0) to (4, 5) is
= 
=
+ 
+ 
+ 
=
1 * 21 + 2 * 15 + 3 * 10 + 4 * 6 = 21 + 30
+ 30 + 24 = 105
Algorithm realization
Declare the constants.
#define MAX 1000001
#define MOD 1000000007
Let’s declare
arrays: fact contains the factorials of numbers modulo MOD, factinv
contains the reciprocals of the factorials of numbers modulo MOD:
fact[n] = n!
mod 1000000007
factinv[n] = n!
-1 mod 1000000007
typedef long long ll;
ll fact[MAX], factinv[MAX];
The pow function finds the power of a number by modulo: xn mod p.
ll pow(ll x, ll n, ll p)
{
if (n == 0) return 1;
if (n % 2 == 0) return pow((x * x) % p, n / 2, p);
return (x * pow(x, n - 1, p)) % p;
}
The inverse function finds the inverse of x
modulo p. Since the number p is prime, then by Fermat’s theorem xp-1 mod p = 1 for every 1 ≤ x < p. The equality can be rewritten as (x * xp-2) mod p = 1, whence the reciprocal of x is xp-2 mod p.
ll inverse(ll x, ll p)
{
return pow(x, p - 2, p);
}
The function Cnk finds the binomial coefficient using
the formula:
=
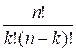
ll Cnk(int n, int k)
{
return ((fact[n] * factinv[k]) % MOD * factinv[n - k]) % MOD;
}
The function ways finds the number of paths on an n * m grid from cell (0, 0) to cell (n, m). Since the
path between the specified points has length n + m, and at the
same time contains m horizontal
segments, the number of paths is equal to .
ll ways(int n, int m)
{
return Cnk(n + m, m);
}
The main part of the program. Fill the arrays of factorials fact
and factinv.
fact[0] =
1;
for (i = 1; i < MAX; i++)
fact[i] = (fact[i - 1] * i) % MOD;
factinv[0]
= 1;
for (i = 1; i < MAX; i++)
factinv[i] = inverse(fact[i], MOD);
Read the input data.
scanf("%d", &tests);
while (tests--)
{
scanf("%d %d %d %d",
&n, &m, &a, &b);
Find the answer using the formula in the variable res.
res = 0;
for (i = 0; i <= m -
b; i++)
res = (res + ways(a - 1, i) * ways(n - a, m
- i)) % MOD;
Print the answer.
printf("%lld\n", res);
}